The function ACF computes an estimate of the autocorrelation function
of a (possibly multivariate) tsibble. Function PACF computes an estimate
of the partial autocorrelation function of a (possibly multivariate) tsibble.
Function CCF computes the cross-correlation or cross-covariance of two columns
from a tsibble.
ACF(
.data,
y,
...,
lag_max = NULL,
type = c("correlation", "covariance", "partial"),
na.action = na.contiguous,
demean = TRUE,
tapered = FALSE
)
PACF(.data, y, ..., lag_max = NULL, na.action = na.contiguous, tapered = FALSE)
CCF(
.data,
y,
x,
...,
lag_max = NULL,
type = c("correlation", "covariance"),
na.action = na.contiguous
)Arguments
- .data
A tsibble
- ...
The column(s) from the tsibble used to compute the ACF, PACF or CCF.
- lag_max
maximum lag at which to calculate the acf. Default is 10*log10(N/m) where N is the number of observations and m the number of series. Will be automatically limited to one less than the number of observations in the series.
- type
character string giving the type of ACF to be computed. Allowed values are
"correlation"(the default),"covariance"or"partial".- na.action
function to be called to handle missing values.
na.passcan be used.- demean
logical. Should the covariances be about the sample means?
- tapered
Produces banded and tapered estimates of the (partial) autocorrelation.
- x, y
a univariate or multivariate (not
ccf) numeric time series object or a numeric vector or matrix, or an"acf"object.
Value
The ACF, PACF and CCF functions return objects
of class "tbl_cf", which is a tsibble containing the correlations computed.
Details
The functions improve the stats::acf(), stats::pacf() and
stats::ccf() functions. The main differences are that ACF does not plot
the exact correlation at lag 0 when type=="correlation" and
the horizontal axes show lags in time units rather than seasonal units.
The resulting tables from these functions can also be plotted using
autoplot.tbl_cf().
References
Hyndman, R.J. (2015). Discussion of "High-dimensional autocovariance matrices and optimal linear prediction". Electronic Journal of Statistics, 9, 792-796.
McMurry, T. L., & Politis, D. N. (2010). Banded and tapered estimates for autocovariance matrices and the linear process bootstrap. Journal of Time Series Analysis, 31(6), 471-482.
See also
Examples
library(tsibble)
#>
#> Attaching package: ‘tsibble’
#> The following objects are masked from ‘package:base’:
#>
#> intersect, setdiff, union
library(tsibbledata)
library(dplyr)
#>
#> Attaching package: ‘dplyr’
#> The following objects are masked from ‘package:stats’:
#>
#> filter, lag
#> The following objects are masked from ‘package:base’:
#>
#> intersect, setdiff, setequal, union
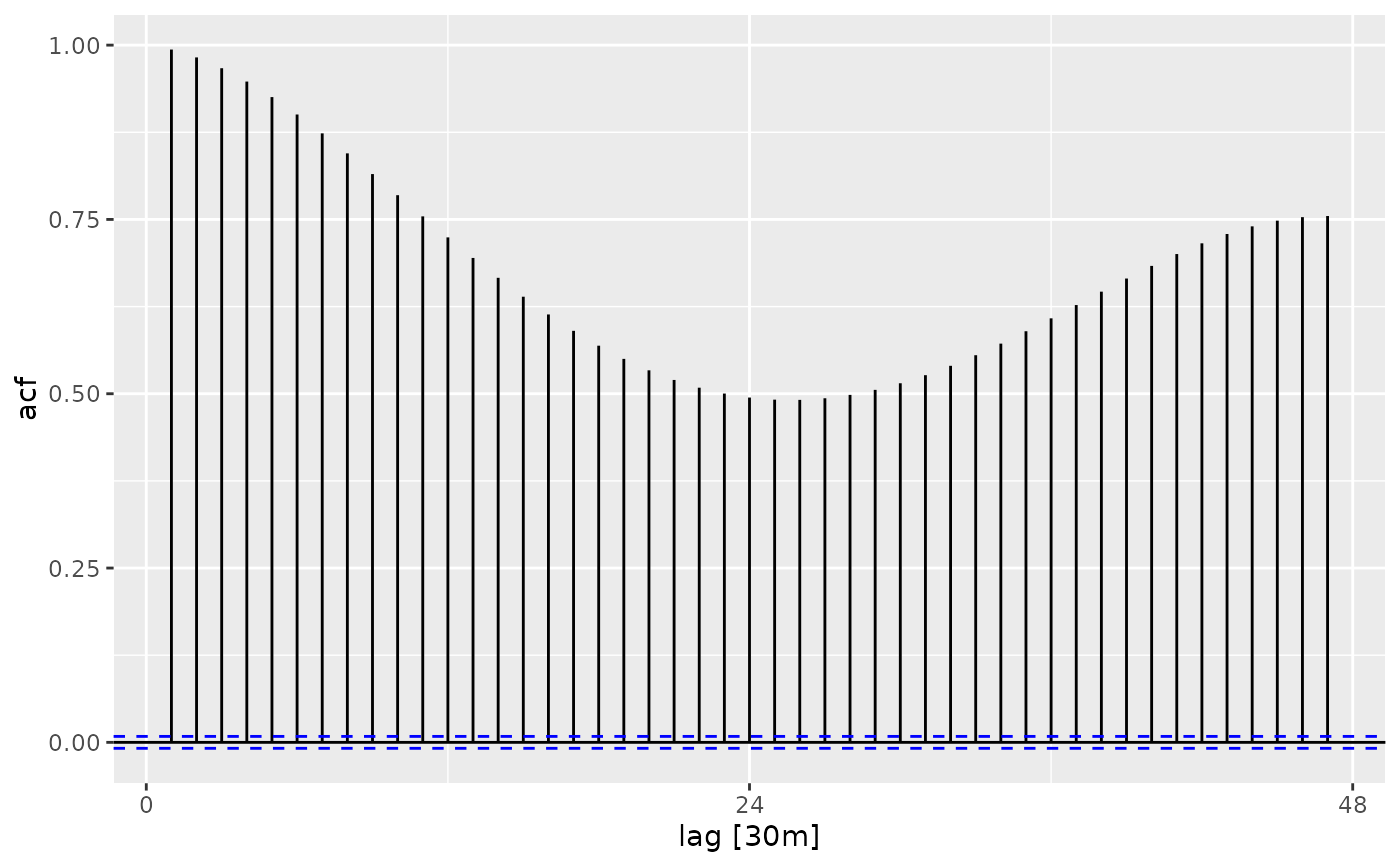
vic_elec %>% ACF(Temperature)
#> # A tsibble: 47 x 2 [30m]
#> lag acf
#> <cf_lag> <dbl>
#> 1 30m 0.994
#> 2 60m 0.982
#> 3 90m 0.967
#> 4 120m 0.948
#> 5 150m 0.925
#> 6 180m 0.901
#> 7 210m 0.873
#> 8 240m 0.845
#> 9 270m 0.815
#> 10 300m 0.785
#> # ℹ 37 more rows
vic_elec %>% ACF(Temperature) %>% autoplot()
 vic_elec %>% PACF(Temperature)
#> # A tsibble: 47 x 2 [30m]
#> lag pacf
#> <cf_lag> <dbl>
#> 1 30m 0.994
#> 2 60m -0.395
#> 3 90m -0.220
#> 4 120m -0.141
#> 5 150m -0.0911
#> 6 180m -0.0611
#> 7 210m -0.0252
#> 8 240m -0.0101
#> 9 270m 0.0152
#> 10 300m 0.0169
#> # ℹ 37 more rows
vic_elec %>% PACF(Temperature) %>% autoplot()
vic_elec %>% PACF(Temperature)
#> # A tsibble: 47 x 2 [30m]
#> lag pacf
#> <cf_lag> <dbl>
#> 1 30m 0.994
#> 2 60m -0.395
#> 3 90m -0.220
#> 4 120m -0.141
#> 5 150m -0.0911
#> 6 180m -0.0611
#> 7 210m -0.0252
#> 8 240m -0.0101
#> 9 270m 0.0152
#> 10 300m 0.0169
#> # ℹ 37 more rows
vic_elec %>% PACF(Temperature) %>% autoplot()
 global_economy %>%
filter(Country == "Australia") %>%
CCF(GDP, Population)
#> # A tsibble: 29 x 3 [1Y]
#> # Key: Country [1]
#> Country lag ccf
#> <fct> <cf_lag> <dbl>
#> 1 Australia -14Y 0.394
#> 2 Australia -13Y 0.427
#> 3 Australia -12Y 0.461
#> 4 Australia -11Y 0.496
#> 5 Australia -10Y 0.530
#> 6 Australia -9Y 0.565
#> 7 Australia -8Y 0.601
#> 8 Australia -7Y 0.637
#> 9 Australia -6Y 0.674
#> 10 Australia -5Y 0.711
#> # ℹ 19 more rows
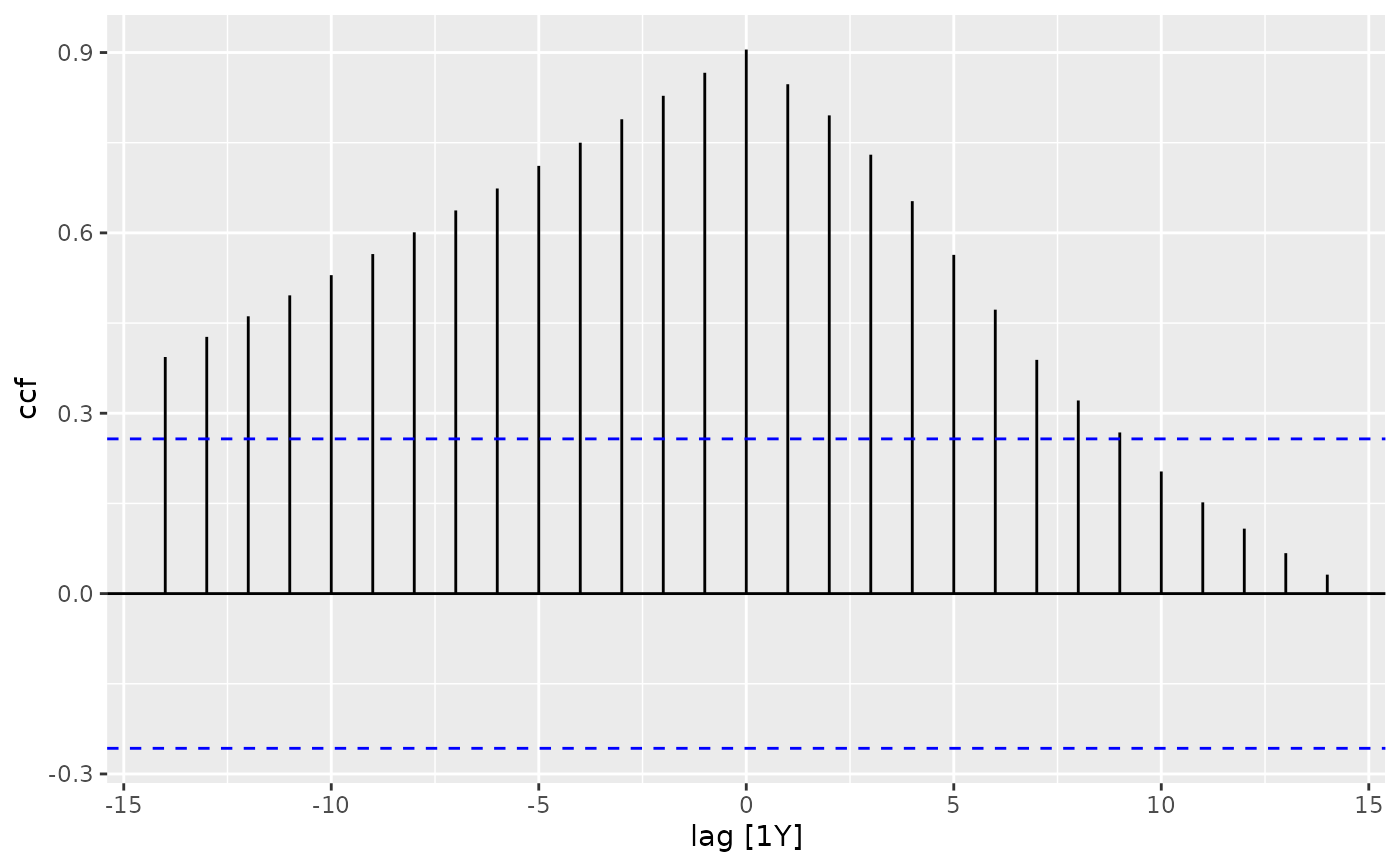
global_economy %>%
filter(Country == "Australia") %>%
CCF(GDP, Population) %>%
autoplot()
global_economy %>%
filter(Country == "Australia") %>%
CCF(GDP, Population)
#> # A tsibble: 29 x 3 [1Y]
#> # Key: Country [1]
#> Country lag ccf
#> <fct> <cf_lag> <dbl>
#> 1 Australia -14Y 0.394
#> 2 Australia -13Y 0.427
#> 3 Australia -12Y 0.461
#> 4 Australia -11Y 0.496
#> 5 Australia -10Y 0.530
#> 6 Australia -9Y 0.565
#> 7 Australia -8Y 0.601
#> 8 Australia -7Y 0.637
#> 9 Australia -6Y 0.674
#> 10 Australia -5Y 0.711
#> # ℹ 19 more rows
global_economy %>%
filter(Country == "Australia") %>%
CCF(GDP, Population) %>%
autoplot()